Activation functions in a deep neural networks

When I first started learning about neural networks, I had a naive assumption: more layers automatically meant a smarter model. Just stack a few layers together, and the network would figure everything out on it's own.
I was genuinely shocked to discover that without activation functions, even a deep network with hundreds of layers mathematically collapses into nothing more than a single linear function.
The Linear Collapse Problem
Let's have a look at a simple neural network without activation functions.
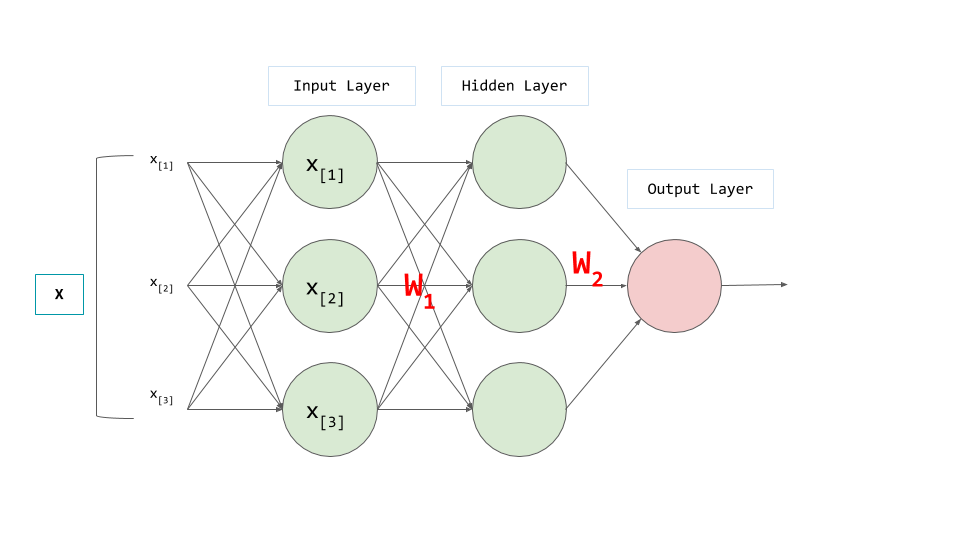
Consider two-layer network:
Layer 1 Output: $$y_1 = W_1X_1 + b_1$$ Layer 2 Output: $$y_2 = W_2(y_1) + b_2$$
Substituting the first equation into the second:
$$y_2 = W_2(W_1X_1 + b_1) + b_2$$ $$y_2 = W_2W_1X_1 + W_2b_1 + b_2$$ $$y_2 = WX + b$$
where
$$W = W_2W_1$$ $$b = W_2b_1 + b_2$$This is equivalent to a single linear transformation. Even if we extend this to 100 layers
$$y_{\text{final}} = W_{\text{final}} \times X + b_{\text{final}}$$
We still get just one linear function, regardless of depth. All those layers collapse into a single line, making the network no more powerful than a linear regression.
Now let's introduce activation functions
Activation functions introduce non-linearlity into the network, preventing this mathematical collapse. They transform the linear output of each neuron before passing it to the next layer.
With activation functions, our network becomes:
$$a_1 = f(W_1X_1 + b_1)$$ $$a_2 = f(W_2a_1 + b_2)$$ $$a_2 = f(W_2(f(W_1X_1 + b_1)) + b_2)$$There’s no algebraic trick that turns this into one linear mapping.
Where f() is the activation function. Now each layer's output is no longer a simple linear combination of the previous layer, breaking the chain of linear transformations.
Common Activation Functions
- ReLU (Rectified Linear Unit)
- Sigmoid
- Tanh (Hyperbolic Tangent)
- Leaky ReLU
- Swish